Обо мне
Обо мне
Обо мне
8.
Формулы приведения
Формулами приведения называются соотношения, с помощью которых значения тригонометрических функций аргументов π/2 ±α; π ±α; 3π/2±α; 2π ±α выражаются через значения sin α, cos α, tg α, ctg α.
Когда мы находим значения тригонометрических функций с помощью единичной окружности, мы используем уже известные табличные значения.
Обратим внимание, что таблица значений тригонометрических функций составлена для углов от 0° до 90°. Это объясняется тем, что значения тригонометрических функций для остальных углов сводятся к значениям тригонометрических функций для острых углов. А формулы, которые позволяют сделать это, называются формулами приведения.
Формулы приведения необходимы для того, чтобы привести вычисления значений тригонометрических функций для любого аргумента к вычислению тригонометрический функций для аргумента [0; π/2]
Формулы приведения основаны на симметрии вращательного движения (см информационная схема «Свойства вращательного движения»)
Мнемоническое правило (мнемоника – искусство запоминания).
Достаточно задать себе два вопроса:
1. Меняется ли функция на кофункцию?
Ответ: Если в формуле присутствуют углы π/2 или 3π/2 - это углы вертикальной оси, киваем головой по вертикали и сами себе отвечаем: «Да», если же присутствуют углы горизонтальной оси π или 2π, то киваем головой по горизонтали и получаем ответ: «Нет».

2. Какой знак надо поставить в правой части формулы?
Ответ: Знак определяем по левой части. Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части.
Для применения формул приведения необходимо помнить правило:
Название функции не меняется, если к аргументу левой части добавляется – π или + π, меняется, если добавляются числа ± π/2 или ± 3π/2.
Знак в правой части определяется знаком левой при 0< t <π/2.

Примеры применения формул приведения
1.Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2 < t < π, тогда (π + t) попадет в третью четверть, а там косинус отрицательный, согласно третьему пункту нашего правила, следует поставить минус перед нашей функцией: cos(t + π) = -cos(t)

2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим,
что 0 < t < π/2, тогда (π/2 + t) попадет во вторую четверть, а там преобразуемая функция синус положительная, согласно третьему пункту нашего правила, следует поставить положительный знак перед нашей функцией:
sin(t + π/2) = cos(t)

3. Преобразуем tg(π + t). Наименование функции остается, т.е. получим tg(t). Далее предположим, что 0 < t < π/2, тогда (π - t) попадет во вторую четверть, а там тангенс отрицательный, согласно третьему пункту нашего правила следует поставить минус перед нашей функцией: tg(t - π) = -tg(t)
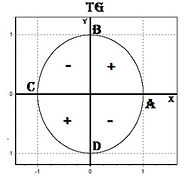
4. Преобразуем ctg(270ͦ + t). Наименование функции изменяется, то есть получим tg(t). Далее предположим что
0 < t < 900, тогда (270ͦ + t) попадет в четвертую четверть, а там преобразуемая функция котангенс отрицательная, согласно третьему пункту нашего правила следует поставить минус перед нашей функцией:
ctg(270ᵒ + t)=-tg(t).
